求助，请大侠帮忙，用matlab求个拟合函数。

caicaptain2

通俗的讲，数据结果受到2个输入变量的影响。经过实验测试，得到了一个表格。怎么获得拟合的函数？
已有数据矩阵8X13，数量不大。

y=f(m,n)=a*m^2+b*n^2+c*m*n+d*m+e*n+f
二次多项式拟合，得想办法得到这个系数abcdef。

https://blog.csdn.net/weixin_46355936/article/details/136448087  这个网页有介绍matlab中的做法。 哪位能帮忙做一下？请私信我。

eric2013

这个稍有点麻烦，得研究下

ME_Engineer

简单的最小二乘拟合问题，把数据贴上，我抽空给你算一下。

你这个函数看起来像是二次曲线啊，椭圆之类的方程？

caicaptain2

ME_Engineer 发表于 2024-6-14 13:45
简单的最小二乘拟合问题，把数据贴上，我抽空给你算一下。

你这个函数看起来像是二次曲线啊，椭圆之类的 ...

为了方便提取数据，数据在这个excel表格里面。
新建 Microsoft Excel 工作表 (2).zip (8.74 KB, 下载次数: 2)

2024-6-14 15:41 上传

点击文件名下载附件

ME_Engineer

a = -7.799379086949847e-06
b = -4.455496631110607e-08
c = 3.8490494044022695e-06
d = 0.0015192728347004471
e = -0.0024760635004740087
f = 1.7949690988566196

你可以先试试，我用拟合后的公式重算了一下，原数据点重算值和实际值最大误差0.04198687339223384。

至于怎么算的，我抽空开个帖子讲讲，大家探讨一下。

庄永

三维曲面拟合

[Python] 纯文本查看 复制代码

import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

x = np.array([0,25,50,75,100,125,150,175,200,225,250,275,300])
y = np.array([303,328,353,378,403,428,453,478])
x, y = np.meshgrid(x, y)
z = np.loadtxt('data.csv', delimiter='\t')

x_flat = x.ravel()
y_flat = y.ravel()
z_flat = z.ravel()

def func(data, a, b, c, d, e, f):
    x, y = data
    return a * x**2 + b * y**2 + c * x * y + d * x + e * y + f

params, _ = curve_fit(func, (x_flat, y_flat), z_flat)

a, b, c, d, e, f = params
print(params)

z_grid = a * x**2 + b * y**2 + c * x * y + d * x + e * y + f

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, label='Data')
ax.plot_surface(x, y, z, alpha=0.5, color='red')

plt.show()

caicaptain2

ME_Engineer 发表于 2024-6-14 17:25
a = -7.799379086949847e-06
b = -4.455496631110607e-08
c = 3.8490494044022695e-06

太棒了！ 考虑到单片机都是单精度浮点，系数取6~7位有效数字后，用excel模拟计算后的结果挺好的。




还有个优化的需求，需要左上角第一个数字拟合后为1.000比较好。因为原始测量数据的左上角精度最高，往右往下精度逐步降低。
不知道能否满足？

caicaptain2

庄永 发表于 2024-6-14 23:51
三维曲面拟合

[mw_shl_code=python,true]import numpy as np

感谢！

用python折腾出来这个，系数与上一个网友的几乎一致，后面我再逐步研究。

[-7.79937910e-06 -4.45450910e-08  3.84904945e-06  1.51927282e-03
-2.47607122e-03  1.79497057e+00]

ME_Engineer

caicaptain2 发表于 2024-6-17 13:45
太棒了！ 考虑到单片机都是单精度浮点，系数取6~7位有效数字后，用excel模拟计算后的结果挺好的。

我想了一下，你的优化需求是说：对一共104个数据点，希望拟合一条曲线，使得后103个点的拟合误差最小，同时要求拟合的曲线必须经过第一个点。

这肯定是可以做到的，我想应该用拉格朗日乘子法就可以实现，但是我对此也不了解，后面如果可能学习一下再试试。你也可以尝试一下；路过的各位大侠，如果有懂的，还请指点一二。

然后你提到测量精度逐步降低，对于这种场景，我觉得用加权最小二乘拟合应该就可以对此优化了，给前面的点赋予更高的权重，拟合得到的曲线就更偏向前面的点。

通过这种思路，可以得到一组系数如下：

a = -8.894136521141365e-06
b = 4.364682267968163e-07
c = 3.2980065451201787e-06
d = 0.002062882301511199
e = -0.0027690861853998956
f = 1.8194118382749287

权重我是随便设的，可能不合适，后面我把代码贴上，你可以自己设计一套权重。

ME_Engineer

补充代码如下：

[Python] 纯文本查看 复制代码

import numpy as np

ms = [0, 25, 50, 75, 100, 125, 150, 175, 200, 225, 250, 275, 300]
ns = [303, 328, 353, 378, 403, 428, 453, 478]

data = [
    [1, 1.110667996, 1.179461615, 1.2333001, 1.263210369, 1.276171486, 1.277168495, 1.269192423, 1.253240279, 1.231306082, 1.202392822, 1.173479561, 1.139581256],
    [0.938185444, 1.042871386, 1.110667996, 1.161515454, 1.192422732, 1.211365902, 1.220338983, 1.216350947, 1.205383848, 1.189431705, 1.170488534, 1.14556331, 1.118644068],
    [0.87337986, 0.975074776, 1.053838485, 1.108673978, 1.14556331, 1.167497507, 1.179461615, 1.181455633, 1.17447657, 1.161515454, 1.142572283, 1.122632104, 1.098703888],
    [0.81555334, 0.913260219, 0.991026919, 1.045862413, 1.084745763, 1.109670987, 1.122632104, 1.127617149, 1.125623131, 1.118644068, 1.10667996, 1.088733799, 1.066799601],
    [0.762711864, 0.858424726, 0.93220339, 0.987038883, 1.02891326, 1.055832502, 1.072781655, 1.080757727, 1.080757727, 1.076769691, 1.066799601, 1.053838485, 1.036889332],
    [0.710867398, 0.800598205, 0.87337986, 0.930209372, 0.97108674, 1, 1.020937188, 1.031904287, 1.037886341, 1.036889332, 1.027916251, 1.014955135, 1],
    [0.664007976, 0.754735793, 0.829511466, 0.885343968, 0.928215354, 0.937188435, 0.959122632, 0.972083749, 0.978065803, 0.979062812, 0.975074776, 0.970089731, 0.96111665],
    [0.608175474, 0.695912263, 0.765702891, 0.819541376, 0.863409771, 0.895314058, 0.917248255, 0.935194417, 0.944167498, 0.948155533, 0.947158524, 0.944167498, 0.935194417],
]

def main():
    M = len(ms)
    N = len(ns)

    A = []
    b = []

    for i in range(N):
        for j in range(M):
            n = ns[i]
            m = ms[j]
            y = data[i][j]

            A.append((m**2, n**2, m*n, m, n, 1))
            b.append((y,))

    A = np.mat(A, dtype=float)
    b = np.mat(b, dtype=float)

    x = (A.T * A).I * A.T * b

    coeff = "abcdef"
    for i in range(len(coeff)):
        print("{} = {}".format(coeff[i], x[i, 0]))

def main2():
    M = len(ms)
    N = len(ns)

    A = []
    b = []
    W = []

    for i in range(N):
        for j in range(M):
            n = ns[i]
            m = ms[j]
            y = data[i][j]

            # weight
            w = (M + N) / (i + j + 1)

            A.append((m**2, n**2, m*n, m, n, 1))
            b.append((y,))
            W.append(w)

    A = np.mat(A, dtype=float)
    b = np.mat(b, dtype=float)
    W = np.diag(W)

    x = (A.T * W * A).I * A.T * W * b

    coeff = "abcdef"
    for i in range(len(coeff)):
        print("{} = {}".format(coeff[i], x[i, 0]))

def test():
    # coeff from main
    # a = -7.799379086949847e-06
    # b = -4.455496631110607e-08
    # c = 3.8490494044022695e-06
    # d = 0.0015192728347004471
    # e = -0.0024760635004740087
    # f = 1.7949690988566196

    # coeff from main2
    a = -8.894136521141365e-06
    b = 4.364682267968163e-07
    c = 3.2980065451201787e-06
    d = 0.002062882301511199
    e = -0.0027690861853998956
    f = 1.8194118382749287

    M = len(ms)
    N = len(ns)

    A = [[0.0 for i in range(M)] for j in range(N)]

    for i in range(N):
        for j in range(M):
            n = ns[i]
            m = ms[j]
            y = a * m**2 + b * n**2 + c * m * n + d * m + e * n + f
            A[i][j] = round(abs(y - data[i][j]) / data[i][j] * 100.0, 2)

    for line in A:
        print(line)

if __name__ == "__main__":
    # main()
    main2()
    # test()

ME_Engineer

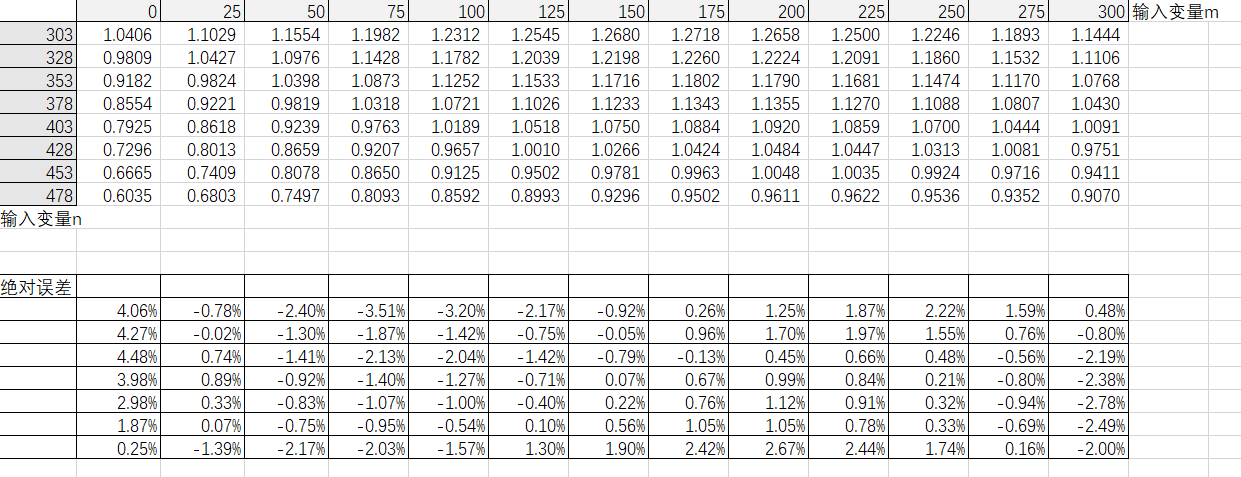
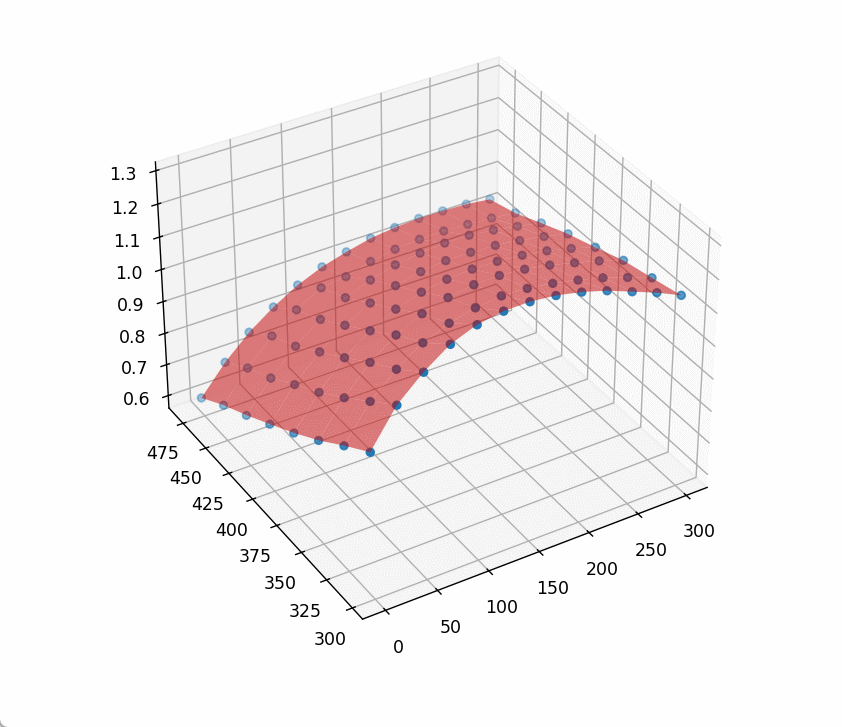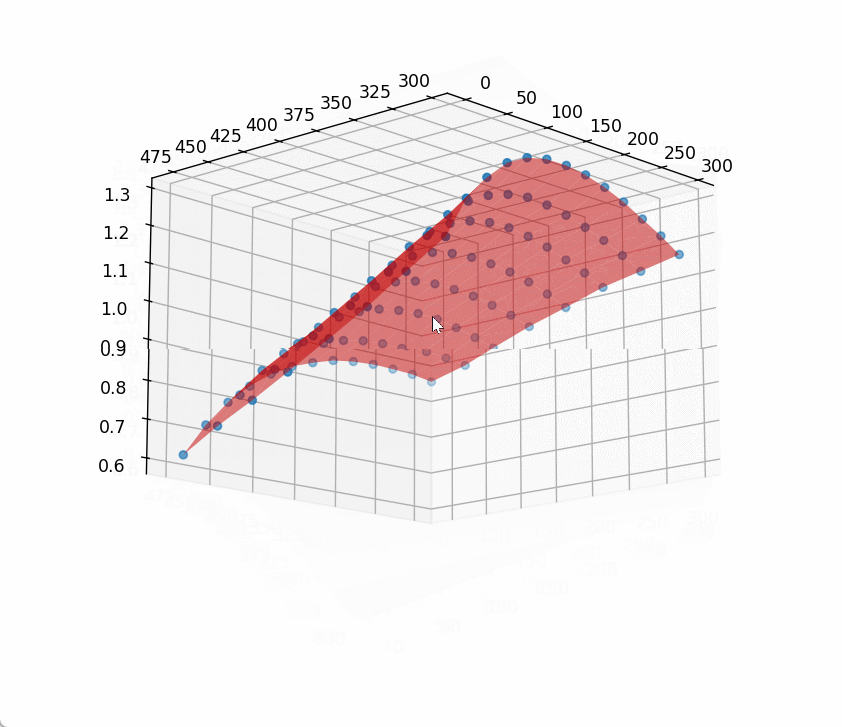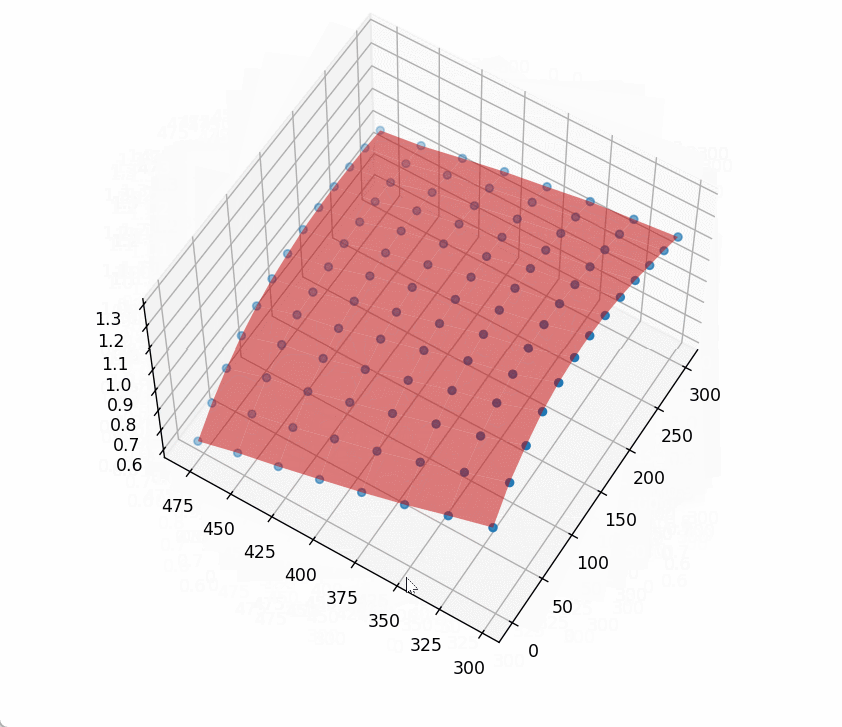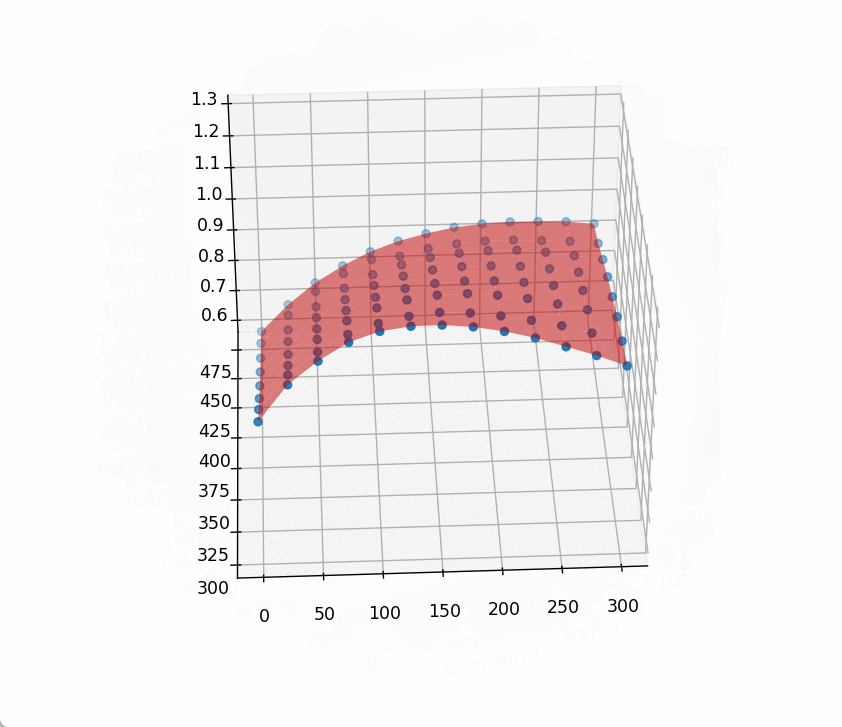
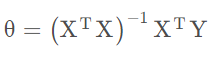对前面的代码，补充一下：

main是做最小二乘拟合，main2则是做加权最小二乘拟合，test是对计算得到的系数做验证测试，计算最大偏差百分比。

使用main的系数，偏差百分比如下：
[4.06, 0.7, 2.04, 2.85, 2.53, 1.7, 0.72, 0.2, 1.0, 1.52, 1.84, 1.35, 0.42]
[4.25, 0.02, 1.18, 1.61, 1.19, 0.62, 0.04, 0.79, 1.41, 1.65, 1.33, 0.67, 0.72]
[4.81, 0.76, 1.34, 1.92, 1.78, 1.22, 0.67, 0.11, 0.38, 0.56, 0.42, 0.5, 1.99]
[4.55, 0.97, 0.92, 1.34, 1.17, 0.64, 0.06, 0.59, 0.88, 0.75, 0.19, 0.74, 2.23]
[3.56, 0.39, 0.89, 1.09, 0.97, 0.38, 0.2, 0.7, 1.04, 0.85, 0.3, 0.89, 2.68]
[2.28, 0.09, 0.86, 1.02, 0.55, 0.1, 0.55, 1.01, 1.01, 0.75, 0.33, 0.68, 2.49]
[0.02, 1.84, 2.62, 2.3, 1.7, 1.38, 1.98, 2.49, 2.73, 2.49, 1.78, 0.16, 2.08]
[1.14, 2.24, 2.09, 1.25, 0.49, 0.44, 1.35, 1.61, 1.79, 1.48, 0.67, 0.95, 3.01]

使用main2的系数，偏差百分比如下：
[2.05, 1.73, 2.39, 2.69, 2.02, 0.93, 0.2, 1.16, 1.91, 2.26, 2.31, 1.4, 0.08]
[2.12, 1.12, 1.58, 1.51, 0.74, 0.07, 0.77, 1.62, 2.15, 2.18, 1.53, 0.41, 1.58]
[2.63, 0.37, 1.75, 1.84, 1.35, 0.58, 0.07, 0.61, 0.98, 0.91, 0.4, 1.02, 3.16]
[2.39, 0.11, 1.28, 1.21, 0.71, 0.01, 0.78, 1.26, 1.38, 0.97, 0.01, 1.49, 3.69]
[1.53, 0.56, 1.12, 0.84, 0.42, 0.34, 0.96, 1.37, 1.5, 0.98, 0.03, 1.83, 4.38]
[0.47, 0.64, 0.88, 0.59, 0.17, 0.95, 1.4, 1.74, 1.49, 0.85, 0.1, 1.76, 4.39]
[1.42, 2.22, 2.33, 1.58, 0.74, 2.46, 3.01, 3.35, 3.28, 2.61, 1.32, 1.03, 4.16]
[2.08, 2.15, 1.37, 0.14, 0.82, 1.8, 2.62, 2.65, 2.48, 1.68, 0.24, 2.17, 5.17]

可见确实是有优化效果的，调整加权函数可能会有更好的效果。

caicaptain2

ME_Engineer 发表于 2024-6-17 20:22
对前面的代码，补充一下：

main是做最小二乘拟合，main2则是做加权最小二乘拟合，test是对计算得到的系 ...

非常感谢！

从最小二乘法的原理上处理这个问题，用了它的解析解 。
为了保证起点数据完全拟合，我可以变换一下，修改变量n的起点为0，而m的起点已经是0了，这样子拟合函数的常数项固定为1（即截距）. 即可保证第一数据确定为1。

愿发红包感谢两位帮忙的网友，方便的话请私信个支付宝或微信号。

ME_Engineer

caicaptain2 发表于 2024-6-18 10:52
非常感谢！

从最小二乘法的原理上处理这个问题，用了它的解析解。

我明白你的意思了。做变换n' = n - 303（即整体平移），则y(0, 0) = f = 1.0，因此系数f已知，只需拟合剩余5个参数就可以了。这倒是一个简便的方法。

[Python] 纯文本查看 复制代码

def main3():
    M = len(ms)
    N = len(ns)

    A = []
    b = []

    for i in range(N):
        for j in range(M):
            n = ns[i] - ns[0]
            m = ms[j]
            y = data[i][j] - 1.0

            A.append((m**2, n**2, m*n, m, n))
            b.append((y,))

    A = np.mat(A, dtype=float)
    b = np.mat(b, dtype=float)

    x = (A.T * A).I * A.T * b

    coeff = "abcde"
    for i in range(len(coeff)):
        print("{} = {}".format(coeff[i], x[i, 0]))
    print("f = 1.0")

结果也确实如此：

[0.0, 3.73, 4.35, 4.6, 3.85, 2.66, 1.39, 0.24, 0.74, 1.39, 1.8, 1.33, 0.37]
[1.01, 2.32, 2.83, 2.76, 1.95, 1.06, 0.24, 0.79, 1.55, 1.88, 1.58, 0.9, 0.57]
[2.32, 0.89, 2.38, 2.53, 2.04, 1.22, 0.47, 0.23, 0.81, 1.02, 0.86, 0.15, 1.78]
[2.76, 0.08, 1.45, 1.49, 1.03, 0.3, 0.55, 1.16, 1.48, 1.32, 0.68, 0.39, 2.1]
[2.38, 0.16, 1.0, 0.89, 0.55, 0.19, 0.86, 1.38, 1.69, 1.4, 0.71, 0.7, 2.78]
[1.57, 0.07, 0.67, 0.59, 0.03, 0.77, 1.24, 1.66, 1.56, 1.14, 0.49, 0.81, 2.99]
[0.36, 1.78, 2.28, 1.79, 1.11, 2.0, 2.55, 2.95, 3.02, 2.54, 1.52, 0.48, 3.18]
[1.42, 2.14, 1.79, 0.84, 0.07, 0.81, 1.6, 1.68, 1.61, 0.99, 0.21, 2.3, 4.91]


不过变换后需要注意数据范围了。