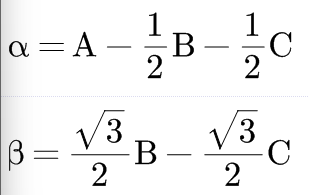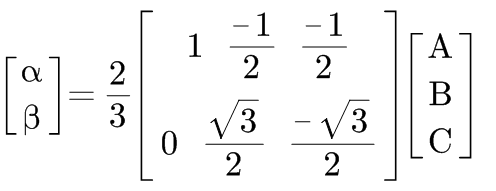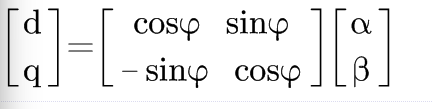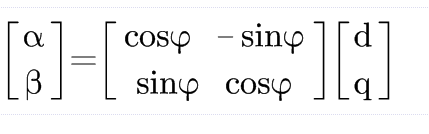FOC电机控制学习记录(二)Clarke变化和Park变换

会飞的猪_2020

FOC电机控制学习记录（零）FOC的意义
https://www.armbbs.cn/forum.php? ... 25689&fromuid=32469
(出处: 硬汉嵌入式论坛)

在这里已经讲述了为什么要进行坐标变化，我们接下来就来看看如何进行坐标变换。

接下来的内容主要参考了《交流电机控制回路设计》叶志鈞以及《电力拖动自动控制系统》阮毅这两本书。


一、clarke变换（从abc变换到αβ）和反clark变换（从αβ变为abc）
abc坐标系是原始的坐标系，也就是三相绕组的坐标系。
二维平面上的一个矢量，不需要三个坐标轴，用两个坐标轴也能表示任意的一个矢量。
αβ是一个正交的坐标系,ABC是夹角呈120°的三相坐标系。
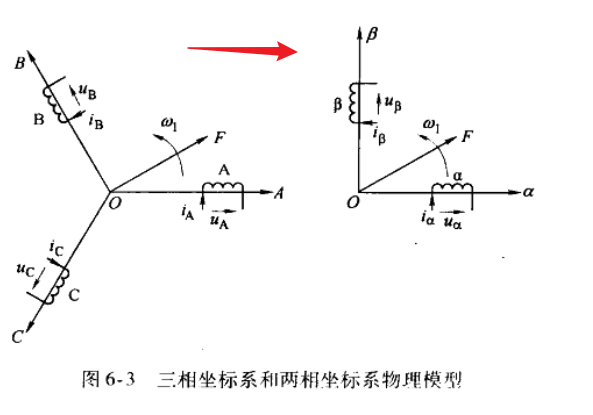
这个我们用几何的知识就能推导出来：

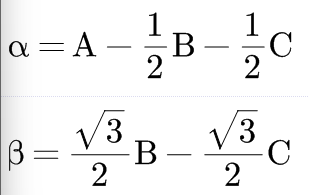
这种式子都可以写成矩阵：

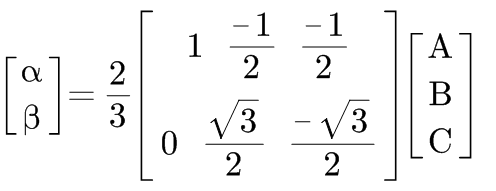
其中为了变换后幅值等效，会在矩阵前面乘上一个2/3的系数。
这里乘上2/3是为了保持幅值相等。因为三相合成之后的矢量的大小是原来的3/2倍，可以参考这里。

FOC电机控制学习记录(一) 空间矢量合成
https://www.armbbs.cn/forum.php? ... 24582&fromuid=32469
(出处: 硬汉嵌入式论坛)


补上零序分量，让这个矩阵变为正交矩阵。（因为A+B+C=0，这个通过几何应该也是可以看出来的）

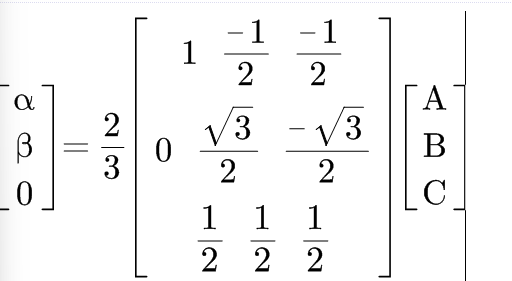
由于正交矩阵的逆矩阵等于矩阵的转置，可以得到反Clark变换。


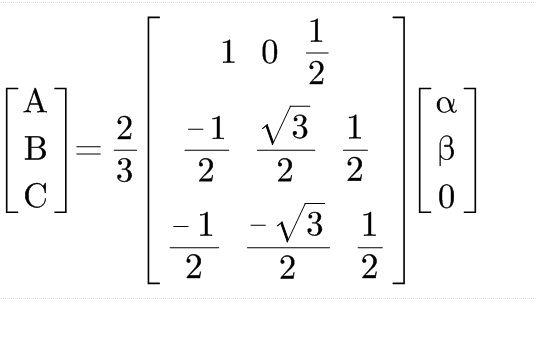
到matlab中验证一下：

[C] 纯文本查看 复制代码

% 设定abc三相的值（相位差均为120°）
t=linspace(0,0.02,100);
va=220*1.414*sin(2*pi*50*t);
vb=220*1.414*sin(2*pi*50*t-2*pi/3);
vc=220*1.414*sin(2*pi*50*t-4*pi/3);

% clarke变换 abc变到αβ
v_alpha=2/3*(1*va-0.5*vb-0.5*vc);
v_beta=2/3*(sqrt(3)/2*vb-sqrt(3)/2*vc);
v_zero=2/3*(0.5*va+0.5*vb+0.5*vc);

% Clarke反变换 αβ变到abc
va1 = v_alpha + 0*v_beta + 0.5*v_zero;
vb1 = -0.5*v_alpha + sqrt(3)/2*v_beta + 0.5*v_zero;
vc1 = -0.5*v_alpha - sqrt(3)/2*v_beta + 0.5*v_zero;

subplot(3,1,1);
plot(t, va, t, vb, t,vc, 'Linewidth', 2);
legend('va','vb','vc');
title('原始坐标系ABC');

subplot(3,1,2);
plot(t, v_alpha, t, v_beta, t,v_zero, 'Linewidth', 2);
legend('v_alpha','v_beta','v_zero');
title('α-β坐标系');

subplot(3,1,3);
plot(t, va1, t, vb1, t,vc1, 'Linewidth', 2);
legend('va1','vb1','vc1');
title('反变换回来之后的ABC');

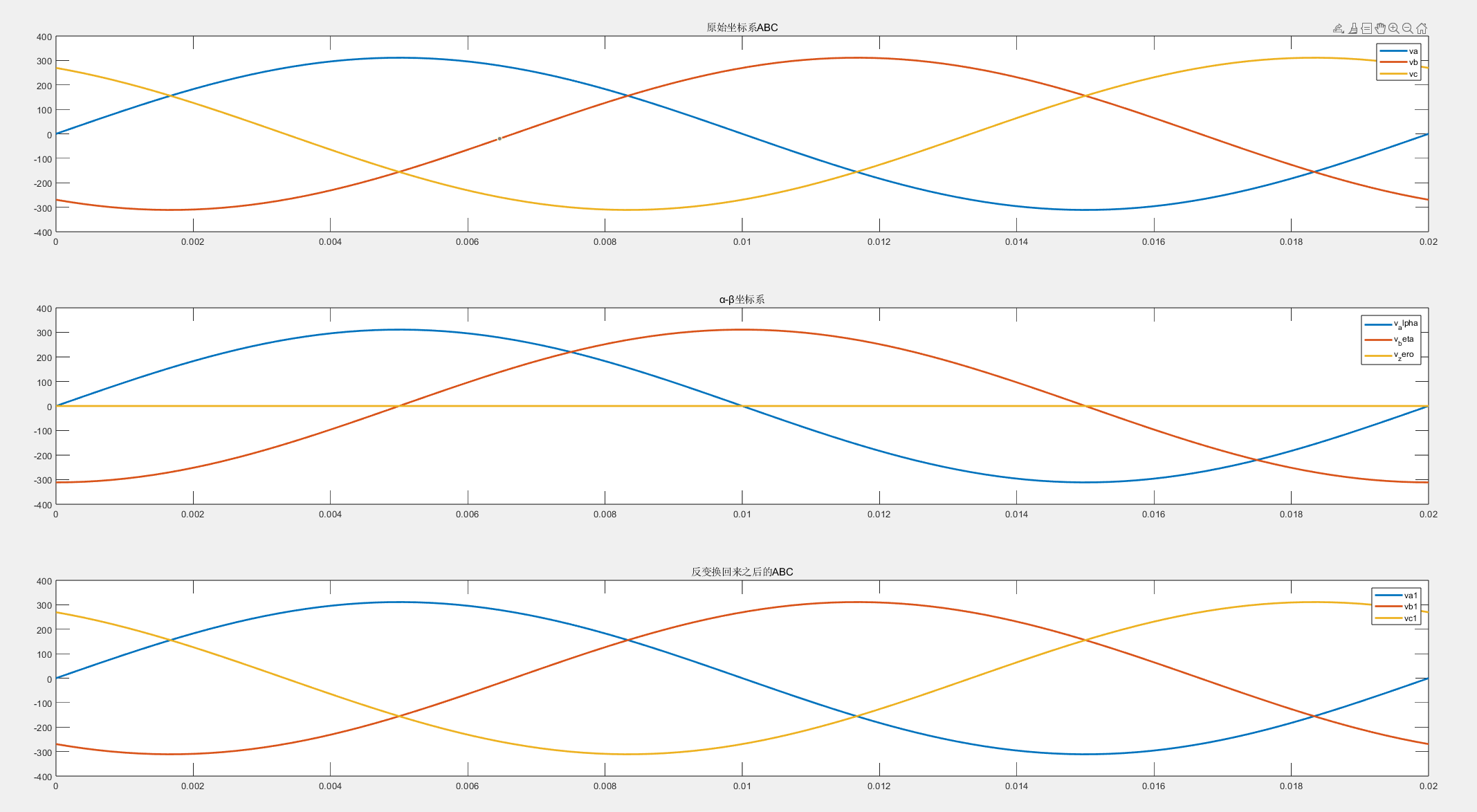
二、park变换（从αβ变换到dq）和反park变换（dq变为αβ）
原始坐标系下的数学模型里面，磁链的一部分组成，是永磁体投射到abc坐标系下得到的。
这部分磁链的值和转子坐标与abc的夹角有关。
如果换到αβ坐标系下，也是一样。会有一个和角度有关系的分量。

为了把这个角度去掉。我们假设存在一个旋转的坐标系（这个坐标系本身会旋转哦），它就是dq坐标系。
它始终跟随转子的转速，和转子保持相对静止。并且让q轴永远超前转子90°
（矢量和转子垂直的时候力矩会是最大的。如果坐标系这样子建立，我们就可以用q轴的电流大小来控制转矩了）

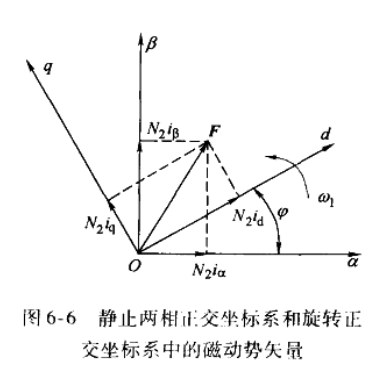
假设αβ坐标系和dq坐标系的夹角为\varphi的话，那么知道αβ就可以根据几何计算出它们在dq轴上的投影：

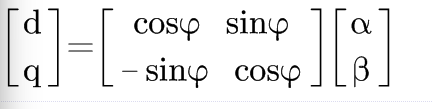
而反park变换则为：

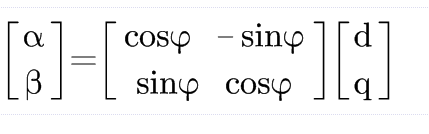
在matlab上运行一下：

[C] 纯文本查看 复制代码

% 设定abc三相的值（相位差均为120°）
t=linspace(0,0.02,100);
va=220*1.414*sin(2*pi*50*t);
vb=220*1.414*sin(2*pi*50*t-2*pi/3);
vc=220*1.414*sin(2*pi*50*t-4*pi/3);

% clarke变换 abc变到αβ
v_alpha=2/3*(1*va-0.5*vb-0.5*vc);
v_beta=2/3*(sqrt(3)/2*vb-sqrt(3)/2*vc);
v_zero=2/3*(0.5*va+0.5*vb+0.5*vc);
% 角度
gamma=2*pi*50*t;
% park αβ变到dq
v_d = cos(gamma).*v_alpha+sin(gamma).*v_beta;
v_q = -sin(gamma).*v_alpha+cos(gamma).*v_beta;

subplot(3,1,1);
plot(t, va, t, vb, t,vc, 'Linewidth', 2);
legend('va','vb','vc');
title('原始坐标系ABC');

subplot(3,1,2);
plot(t, v_alpha, t, v_beta, t,v_zero, 'Linewidth', 2);
legend('v_alpha','v_beta','v_zero');
title('α-β坐标系');

subplot(3,1,3);
plot(t, v_d, t, v_q, 'Linewidth', 2);
ylim([-350 50]);
legend('v_d','v_q');
title('dq坐标系');

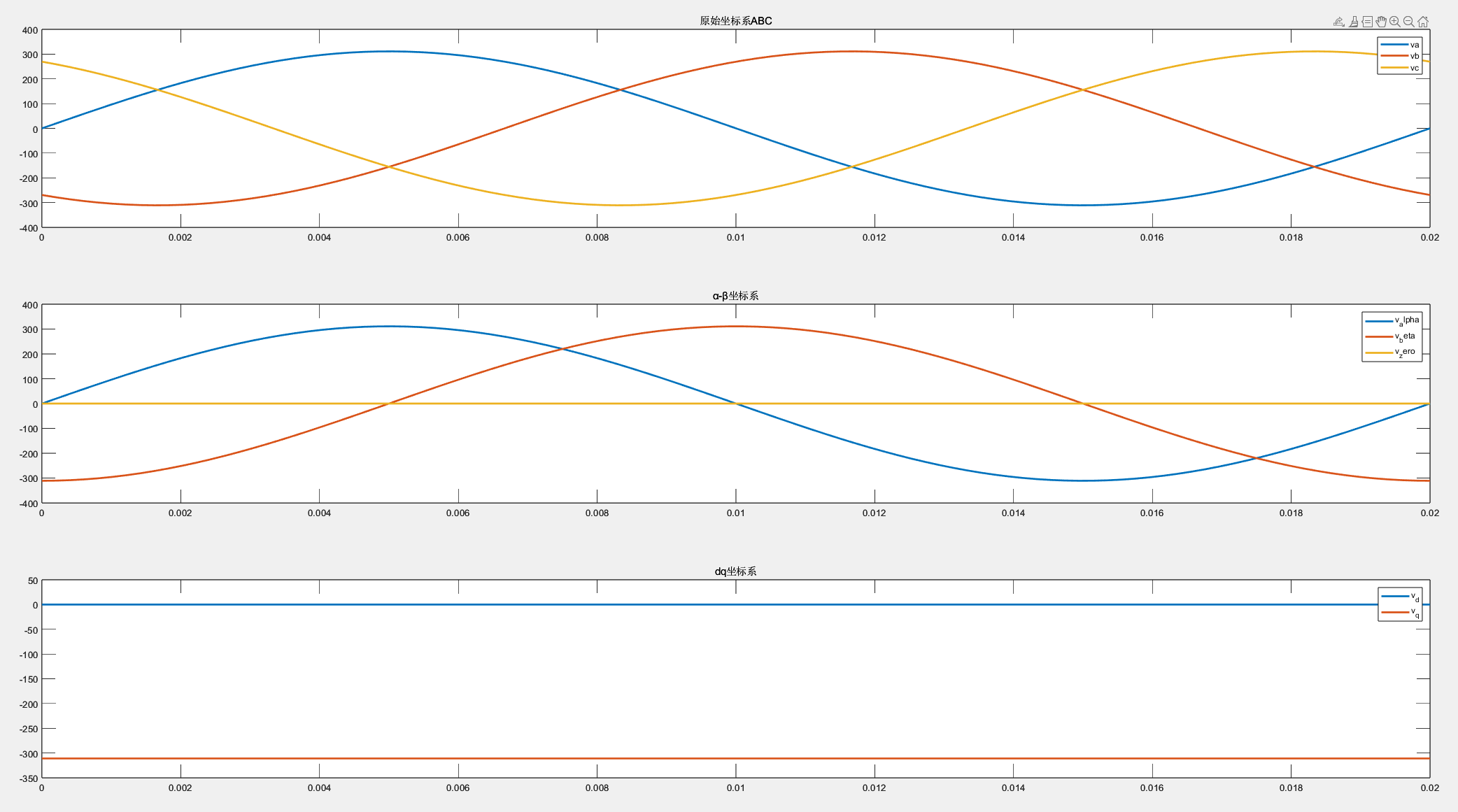
我们可以发现d轴电流为0，q轴电流保持不变。



这部分内容是比较简单的。用几何的知识推导一下就可以得出了。网上的视频也很多。
对于线性代数部分，实际上学过计算机图像处理的朋友，就知道，这个矩阵实际上就是一个坐标变换。
对于矩阵的意义，不了解的朋友，我可以推荐一个视频：
【【熟肉】线性代数的本质 - 03 - 矩阵与线性变换】 https://www.bilibili.com/video/B ... 443339f39608362cd6b

soyshell

一直追楼主的这个系列！

morning_enr6U