|
|

楼主 |
发表于 2015-4-27 10:56:09
|
显示全部楼层
39.2 切比雪夫滤波器的设计
切比雪夫(Chebyshev)滤波器分为Chebyshev I型和Chebyshev II型,分别具有通带等纹波和阻带等纹波性能。
39.2.1 cheby1函数
功能:用来设计Chebyshev(切比雪夫)I型滤波器(通带等纹波)。
语法:[b,a] = cheby1(n, Rp, Wn);
[b,a] = cheby1(n, Rp, Wn, 'ftype');
说明:cheby1函数可以设计低通,带通,高通和带阻Chebyshev I型数字滤波器,其通带内为等纹波,阻带内为单调。Chebyshev I型滤波器的下降斜度比Chebyshev II型大,但其代价是在通带内纹波较大。
[b,a] = cheby1(n, Rp, Wn);可以设计n阶低通Chebyshev I型数字滤波器,其中RP用来确定通带内的纹波,Wn为改滤波器的截止频率。
当Wn=[W1, W2]时,cheby1函数可产生一个2n的数字带通滤波器,其通带为W1<W<W2。
[b,a] = cheby1(n, Rp, Wn, 'ftype');可用来设计n阶高通或带阻滤波器,其中Rp和Wn同上,ftype的定义与butter相同。
39.2.2 cheby1ord函数
功能:用来选择Chebyshev I型滤波器的阶数。
语法:[n, Wn] = cheb1ord(WP, WS, RP, Rs);
说明:cheb1ord函数可以在给定滤波器性能的情况下,选择Chebyshev I型数字滤波器的最小阶数,其中Wp和Ws分别是通带和阻带的截止频率,其值为0Wp(或Ws)1。Rp和Rs分别是通带和阻带区的波纹系数。
[n, Wn] = cheb1ord(WP, WS, RP, Rs);可以得到低通、高通、带通和带阻滤波器的最小阶数。
利用cheblord函数,除了可以得到Chebyshev I型数字滤波器的最小阶数n外,还可以得到截止频率Wn,再利用cheby1函数可产生满足指定性能的滤波器,使滤波器通带(0, Wp)内的纹波系数小于Rp,阻带(WS, 1)内衰减系数大于RS
39.2.3 cheby2函数
功能:用来设计Chebyshev(切比雪夫)I型滤波器(通带等纹波)。
语法:[b,a] = cheby1(n, Rp, Wn);
[b,a] = cheby1(n, Rp, Wn, 'ftype');
说明:cheby2函数与cheby1函数基本相同,只是用cheby2函数所设计的滤波器,其通带内为单调的,阻带内为等波纹,由RS指定阻带内的波纹。
cheby2函数可以设计低通,带通,高通和带阻Chebyshev II型数字滤波器。
39.2.4 cheby2ord函数
功能:用来选择Chebyshev II型滤波器的阶数。
语法:[n, Wn] = cheb2ord(WP, WS, RP, Rs);
说明:cheb2ord函数与cheb2函数类似,可以利用该函数确定Chebyshev II型数字滤波器的最小阶数n和截止频率Wn。
cheb2ord函数和cheb2函数配合使用,可设计出最低阶数的Chebyshev II型数字滤波器。
39.2.5 切比雪夫I型低通滤波器设计
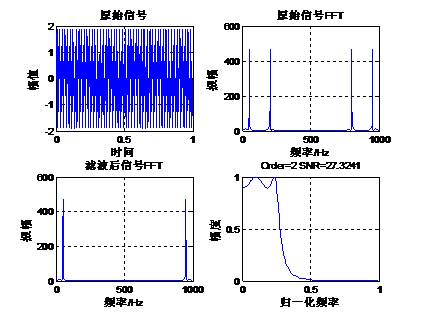
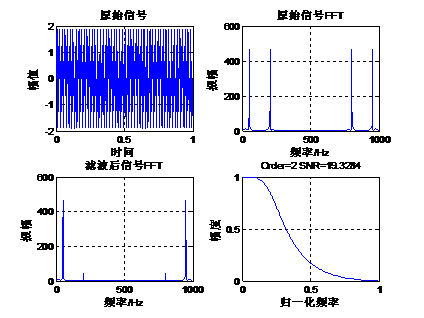
下面我们通过一个实例来讲解切比雪夫I型低通滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成,将200Hz的正弦波当做噪声滤掉,下面通过函数cheby1设计一组低通滤波器系数,其阶数是4,截止频率为0.25(也就是125Hz),采样率1Kbps,通带波纹1db。Matlab运行代码如下:- fs=1000; %设置采样频率 1k
- N=1024; %采样点数
- n=0:N-1;
- t=0:1/fs:1-1/fs; %时间序列
- f=n*fs/N; %频率序列
-
- x1=sin(2*pi*50*t); %信号
- x2=sin(2*pi*200*t); %噪声
- x=x1+x2; %信号混合
-
- subplot(221);
- plot(t,x); %绘制原始信号
- xlabel('时间');
- ylabel('幅值');
- title('原始信号');
- grid on;
-
- subplot(222);
- y=fft(x,N); %绘制原始信号的幅频响应
- plot(f,abs(y));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('原始信号FFT');
- grid on;
-
- subplot(223);
- Wc=2*125/fs; %设置截止频率125Hz
- [b,a]=cheby1(4, 3, Wc); %获取2阶IIR滤波系数
- % y2=filter(b,a,x);
- y2=filtfilt(b,a,x); %计算滤波后的波形y2
- y3=fft(y2,N); %滤波后波形的幅频响应
- plot(f,abs(y3));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('滤波后信号FFT');
- grid on;
-
- [H,F]=freqz(b,a,512);
- subplot(224);
- plot(F/pi,abs(H));
- xlabel('归一化频率'); %绘制绝对幅频响应
- ylabel('幅度');
- Ps=sum(x1.^2); %信号的总功率
- Pu=sum((y2-x1).^2); %剩余噪声的功率
- SNR=10*log10(Ps/Pu); %信噪比
- title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
- grid on;
Matlab计算结果如下:
从滤波的效果来看,4阶的切比雪夫I型滤波效果还是比较好的。
39.2.6 切比雪夫I型高通滤波器设计
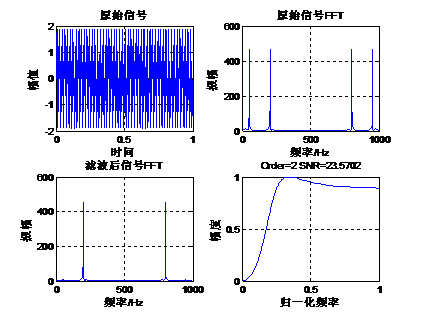
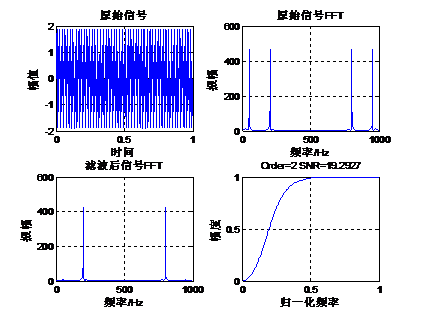
下面我们通过一个实例来讲解切比雪夫I型高通滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成,将50Hz的正弦波当做噪声滤掉,下面通过函数cheby1设计一组高通滤波器系数,其阶数是2,截止频率为0.25(也就是125Hz),采样率1Kbps,通带波纹1db。Matlab运行代码如下:- fs=1000; %设置采样频率 1k
- N=1024; %采样点数
- n=0:N-1;
- t=0:1/fs:1-1/fs; %时间序列
- f=n*fs/N; %频率序列
-
- x1=sin(2*pi*50*t); %噪声
- x2=sin(2*pi*200*t); %信号
- x=x1+x2; %信号混合
-
- subplot(221);
- plot(t,x); %绘制原始信号
- xlabel('时间');
- ylabel('幅值');
- title('原始信号');
- grid on;
-
- subplot(222);
- y=fft(x,N); %绘制原始信号的幅频响应
- plot(f,abs(y));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('原始信号FFT');
- grid on;
-
- subplot(223);
- Wc=2*125/fs; %设置截止频率125Hz
- [b,a]=cheby1(2, 1, Wc, 'high'); %获取2阶IIR滤波系数
- % y2=filter(b,a,x);
- y2=filtfilt(b,a,x); %计算滤波后的波形y2
- y3=fft(y2,N); %滤波后波形的幅频响应
- plot(f,abs(y3));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('滤波后信号FFT');
- grid on;
-
- [H,F]=freqz(b,a,512);
- subplot(224);
- plot(F/pi,abs(H));
- xlabel('归一化频率'); %绘制绝对幅频响应
- ylabel('幅度');
- Ps=sum(x2.^2); %信号的总功率
- Pu=sum((y2-x2).^2); %剩余噪声的功率
- SNR=10*log10(Ps/Pu); %信噪比
- title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
- grid on;
Matlab运行结果如下:
39.2.7 切比雪夫I型带通滤波器设计
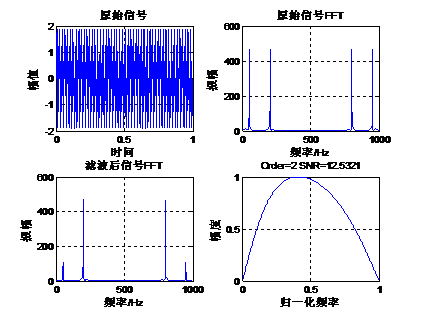
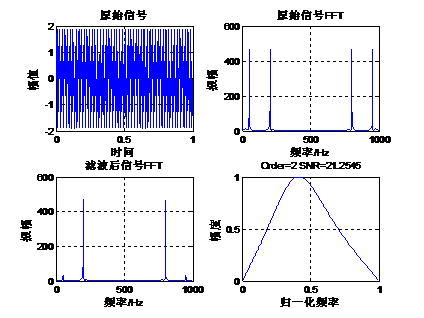
下面我们通过一个实例来讲解切比雪夫I型带通滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成,将50Hz的正弦波当做噪声滤掉,下面通过函数cheby1设计一组带通滤波器系数,其阶数是2,通带为125Hz到300Hz,采样率1Kbps,通带纹波1db。Matlab运行代码如下:- fs=1000; %设置采样频率 1k
- N=1024; %采样点数
- n=0:N-1;
- t=0:1/fs:1-1/fs; %时间序列
- f=n*fs/N; %频率序列
-
- x1=sin(2*pi*50*t); %噪声
- x2=sin(2*pi*200*t); %信号
- x=x1+x2; %信号混合
-
- subplot(221);
- plot(t,x); %绘制原始信号
- xlabel('时间');
- ylabel('幅值');
- title('原始信号');
- grid on;
-
- subplot(222);
- y=fft(x,N); %绘制原始信号的幅频响应
- plot(f,abs(y));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('原始信号FFT');
- grid on;
-
- subplot(223);
- Wn=[125*2 300*2]/fs; %设置通带125Hz到300Hz
- [b,a]=cheby1(1,1,Wn); %注意第一个参数虽然是1,但生成的却是2阶IIR滤波器系数
- % y2=filter(b,a,x);
- y2=filtfilt(b,a,x); %计算滤波后的波形y2
- y3=fft(y2,N); %滤波后波形的幅频响应
- plot(f,abs(y3));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('滤波后信号FFT');
- grid on;
-
- [H,F]=freqz(b,a,512);
- subplot(224);
- plot(F/pi,abs(H));
- xlabel('归一化频率'); %绘制绝对幅频响应
- ylabel('幅度');
- Ps=sum(x2.^2); %信号的总功率
- Pu=sum((y2-x2).^2); %剩余噪声的功率
- SNR=10*log10(Ps/Pu); %信噪比
- title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
- grid on;
Matlab的计算结果如下:
从滤波的效果来看,2阶的带通滤波器效果不够好,出现这种情况的时候,需要大家去重新的调节截止频率,滤波器阶数和通带波纹。
39.2.8 切比雪夫I型带阻滤波器设计
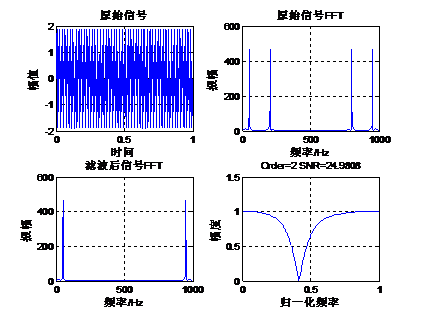
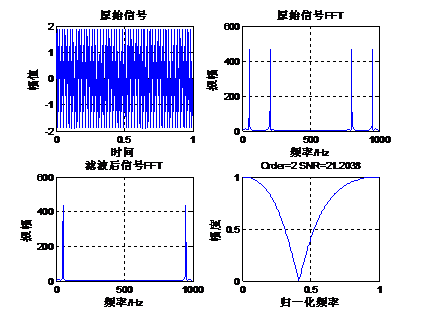
下面我们通过一个实例来讲解切比雪夫I型带阻滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成,将200Hz的正弦波当做噪声滤掉,下面通过函数cheby1设计一组带阻滤波器系数,其阶数是2,阻带为125Hz到300Hz,采样率1Kbps,通带波纹1db。Matlab运行代码如下:- fs=1000; %设置采样频率 1k
- N=1024; %采样点数
- n=0:N-1;
- t=0:1/fs:1-1/fs; %时间序列
- f=n*fs/N; %频率序列
-
- x1=sin(2*pi*50*t); %信号
- x2=sin(2*pi*200*t); %噪声
- x=x1+x2; %信号混合
-
- subplot(221);
- plot(t,x); %绘制原始信号
- xlabel('时间');
- ylabel('幅值');
- title('原始信号');
- grid on;
-
- subplot(222);
- y=fft(x,N); %绘制原始信号的幅频响应
- plot(f,abs(y));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('原始信号FFT');
- grid on;
-
- subplot(223);
- Wn=[125*2 300*2]/fs; %设置阻带125Hz到300Hz
- [b,a]=cheby1(1,1,Wn, 'stop'); %注意第一个参数虽然是1,但生成的却是2阶IIR滤波器系数
- % y2=filter(b,a,x);
- y2=filtfilt(b,a,x); %计算滤波后的波形y2
- y3=fft(y2,N); %滤波后波形的幅频响应
- plot(f,abs(y3));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('滤波后信号FFT');
- grid on;
-
- [H,F]=freqz(b,a,512);
- subplot(224);
- plot(F/pi,abs(H));
- xlabel('归一化频率'); %绘制绝对幅频响应
- ylabel('幅度');
- Ps=sum(x1.^2); %信号的总功率
- Pu=sum((y2-x1).^2); %剩余噪声的功率
- SNR=10*log10(Ps/Pu); %信噪比
- title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
- grid on;
Matlab计算结果如下:
从滤波的效果来看,2阶带阻滤波的效果较好。 |
|








 发表于 2015-4-27 10:43:06
发表于 2015-4-27 10:43:06
 楼主
楼主