|
|
这种方法最早被记载于中国的九章算术中。而在欧洲则是牛顿最先发现这种方法。Carl Friedrich Gauss(高斯)于1810年发明了一种在19世纪被广为接受的(特别是对于当时辛勤工作的手算员)的用于symmetric elimination的记法,这种记法被手算员们广泛应用于解决正常方程的最小二乘问题。而此词条的高斯-若尔当消元法的命名中的“若尔当”则来源于1888年德国数学家Wilhelm Jordan发现了这种高斯消元法的变体。有趣的是Clasen在同年出版的作品中也提到了相同的方法。这个事情更多地被认为是两人分别独立地发现了此方法。
- /*--------------------------------------------------------------------------------------------------------------
- * Matrix Inverse can be solved using elementary row operations.
- *
- * Gauss-Jordan Method:
- *
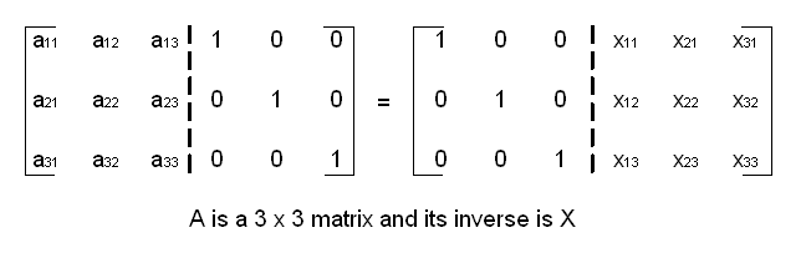
- * 1. First combine the identity matrix and the input matrix separated by a bar to form an
- * augmented matrix as follows:
- * _ _ _ _
- * | a11 a12 | 1 0 | | X11 X12 |
- * | | | = | |
- * |_ a21 a22 | 0 1 _| |_ X21 X21 _|
- *
- * 2. In our implementation, pDst Matrix is used as identity matrix.
- *
- * 3. Begin with the first row. Let i = 1.
- *
- * 4. Check to see if the pivot for column i is the greatest of the column.
- * The pivot is the element of the main diagonal that is on the current row.
- * For instance, if working with row i, then the pivot element is aii.
- * If the pivot is not the most significant of the columns, exchange that row with a row
- * below it that does contain the most significant value in column i. If the most
- * significant value of the column is zero, then an inverse to that matrix does not exist.
- * The most significant value of the column is the absolute maximum.
- *
- * 5. Divide every element of row i by the pivot.
- *
- * 6. For every row below and row i, replace that row with the sum of that row and
- * a multiple of row i so that each new element in column i below row i is zero.
- *
- * 7. Move to the next row and column and repeat steps 2 through 5 until you have zeros
- * for every element below and above the main diagonal.
- *
- * 8. Now an identical matrix is formed to the left of the bar(input matrix, pSrc).
- * Therefore, the matrix to the right of the bar is our solution(pDst matrix, pDst).
- *----------------------------------------------------------------------------------------------------------------*/
|
|









 发表于 2020-3-22 00:12:29
发表于 2020-3-22 00:12:29

 楼主
楼主 发表于 2020-4-27 22:55:52
发表于 2020-4-27 22:55:52
