|
|
为了说明频谱泄露的问题,这里我们具一个求解方波FFT变换的例子。在matlab中运行如下代码:
Fs = 256; % 采样率
N = 256; % 采样点数
n = 0:N-1; % 采样序列
t = 0:1/Fs:1-1/Fs; % 时间序列
x = square(2*pi*30*t, 50); %原始信号
y = fft(x); %对原始信号做FFT变换
M = abs(y); %求FFT转换结果的模值
plot(n, M); %绘制FFT转换模值的曲线
运行代码,输出结果如下:
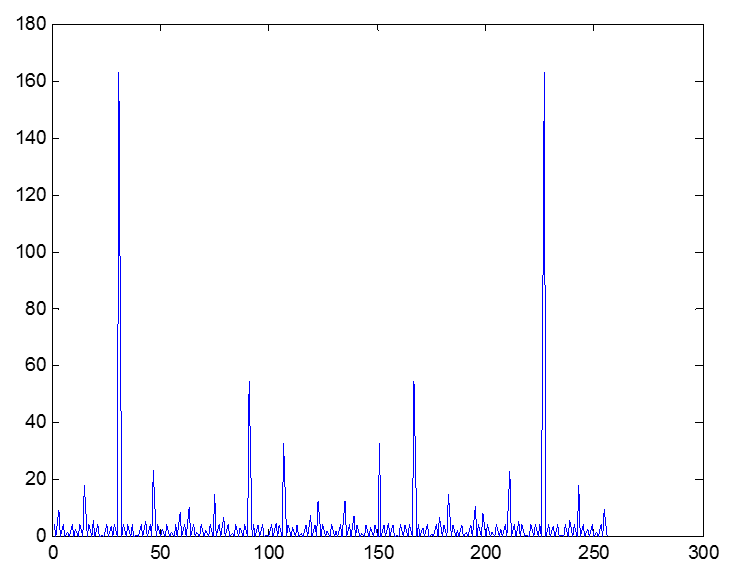
与方波的理论计算值相比,上面的幅频响应图中出现了很多小毛刺,其实这个就是频谱泄露的结果导致的。
下面就说说什么是频谱泄露:
对于频率为fs的正弦序列,它的频谱应该只是在fs处有离散谱。但是,在利用DFT求它的频谱做了截短,结果使信号的频谱不只是在fs处有离散谱,而是在以fs为中心的频带范围内都有谱线出现,它们可以理解为是从fs频率上“泄露”出去的,这种现象称 为频谱“泄露"(结合上面的例子就更形象了)。
在实际问题中遇到的离散时间序列x(n)通常是无限长序列,因而处理这个序列的时候需要将它截短。截短相当于将序列乘以窗函数w(n)。根据频域卷积定理,时域中x(n)和w(n)相乘对应于频域中它们的离散傅立叶变换X(jw)和W(jw)的卷积。因此,x(n)截矩后的频谱不同于它以前的频谱。
为了减小频谱“泄露”的影响,往往在FFT处理中采用加窗技术,典型的加窗序列有Hamming、Blackman、Gaussian等窗序列。此外,增加窗序列的长度也可以减少频谱“泄露”。
时域上乘上窗函数,相当于频域进行卷积。长度为无穷长的常数窗函数,频域为delta函数,卷积后的结果和原来一样。如果是有限矩形窗,频域是Sa函数,旁瓣电平起伏大,和原频谱卷积完,会产生较大的失真。
窗的频谱,越像delta函数(主瓣越窄,旁瓣越小),频谱的还原度越高。于是,就产生了那么多bt的窗函数。加窗就不可避免频谱泄漏,典型的加权序列有Hamming、Blackman、Gaussian等窗序列主要是为了降低降低旁瓣,对于降低频谱泄漏效果远不如增加窗序列的长度明显。
周期信号加窗后做DFT仍然有可能引起频谱泄露,设fs为采样频率,N为采样序列长度,分析频率为:m*fs/N(m=0,1....),以cos函数为例,设其频率为f0,如果 f0不等于m*fs/N,就会引起除f0以外的其他m*fs/N点为非零值,即出现了泄露。
DFT作为有限长的运算,对于无限长的信号必须要进行一定程度的截断,既然信号已经不完整了,那么截断后的信号频谱肯定就会发生畸变,截断由窗函数来完成,实际的窗函数都存在着不同幅度的旁瓣,所以在卷积时,除了离散点的频率上有幅度分量外,在相邻的两个频率点之间也有不同程度的幅度,这些应该就是截断函数旁瓣所造成的。
|
|









 发表于 2020-5-17 15:48:37
发表于 2020-5-17 15:48:37

